שיטת הניתוח Wavelet ("תורת הגלונים") הינה אוסף של כלים וטכניקות לניתוח אותות. בין היתר, היא משמשת לדחיסת תמונות של טביעות אצבע במאגרי ה-FBI, הפחתת רעש באותות ECG או בתמונות ועוד. כדי להבין מה יתרונות שיטת הניתוח הזו על השיטות המוכרות והוותיקות יותר, תובא תחילה סקירה של שיטות אלה וחסרונותיהן.
ניתוח פוריה
ניתוח פוריה, מהמאה ה-19, מפרק סיגנל למרכיבים סינוסואידים בתדרים שונים. זו בעצם טכניקה מתמטית להתמרה של ההסתכלות שלנו על הסיגנל ממישור הזמן למישור התדר. להרבה אותות זה ניתוח שימושי, כי התכולה התדרית של האות היא מאוד חשובה.
אז מה הבעיה?
הבעיה בניתוח פוריה היא שכאשר מסתכלים על התמרת פוריה של סיגנל, אי אפשר לדעת בדיוק מתי אירוע מסויים התרחש. אם הסיגנל סטציונרי, כלומר אם מאפייניו לא משתנים ממש לאורך הזמן, החסרון שהוזכר לא ממש קריטי. אולם, רוב הסיגנלים המעניינים הם לא כאלה, אלא מכילים סחיפות, מגמות, שינויים פתאומיים, אי רציפות של נגזרות מסדר גבוה, והתחלות וסיומים של ארועים. וניתוח פוריה לא מתאים בשביל לאתר כאלה דברים.
STFT
דניס גאבור הציע ב-1946 דרך להתגבר על החסרון הנ"ל של ניתוח פוריה – והיא להשתמש בניתוח הזה על מקטעים של הסיגנל. בעזרת חלון מתאים מקבלים את המקטעים השונים, ועל כ"א מהם עושים את ניתוח פוריה (שבשיטה הקודמת בוצע על האות כולו). האדפטדציה הזו נקראת Short-Time Fourier Transform, והיא ממפה את הסיגנל לפונקציה בשני משתנים: תדר וזמן. ה-STFT הוא סוג של פשרה בין התבוננות על הסיגנל המבוססת על הזמן ובין התבוננות עליו המבוססת על התדר. היא מאפשרת קבלת מידע גם על "מה היו התדרים" וגם על "מתי היו התדרים האלה".
אז מה הבעיה?
הדיוק של המידע הזה מוגבל, והוא תלוי בגודל החלון שבו עושים שימוש. וברגע שבוחרים את גודל החלון – החלון קבוע, יהיו התדרים אשר יהיו. וזו בעיה כיוון שלניתוח של אותות רבים נדרשת גישה יותר גמישה – כזו שבה אפשר לשנות את גודל החלון כדי לקבוע בדיוק רב יותר את זמן או את התדר.
אז מה הפתרון? ניחשתם נכון – ניתוח Wavelet !
ניתוח Wavelet
זהו בעצם השלב הלוגי הבא – טכניקה של עבודה עם חלונות עם גודל משתנה. ניתוח Wavelet מאפשר להשתמש באינטרוולי זמן ארוכים היכן שמעניינת אותה האינפורמציה בתדרים הנמוכים, ובאינטרוולים קצרים יותר היכן שמעניינת אותה האינפורמציה בתדרים הגבוהים. לגלונים, אם כך, יש היבטים של scaling והיבטים של זמן.
היכולת הזו לבצע ניתוח מקומי (ניתוח של אזור מסויים בסיגנל הגדול) חשובה מאוד - קחו לדוגמה גל סינוס בתדר Wo עם עיוות קטנטן, למשל – אי רציפות, שזה משהו שבהחלט יכול לקרות בעולם האמיתי, למשל בגלל פלקטואציה חשמלית או מתג רועש. התמרת פוריה של הסיגנל הזה, שאותה מקבלים ב-MATLAB ע"י פקודת fft, תיתן לנו שני פיקים, ב-Wo וב-Wo-. ניתוח Wavelet, לעומת זאת, יראה בבירור גם את המיקום המדוייק של העיוות על ציר הזמן.
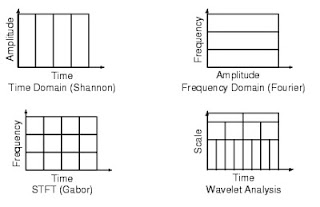
להלן סיכום של ארבע הצורות להצגת סיגנל שעסקנו בהן – בזמן, בתדר, במישור גאבור ובמישור Wavelet:
בעוד ניתוח פוריה מפרק סיגנל לסינוסואידות בתדרים שונים, ניתוח Wavelet מפרק סיגנל לגרסאות מוזזות ובעלות סקאלה שונה של גלון האם, גלון המקור. גלון הינו אות בעל משך סופי וממוצע אפס. סינוסואידות, שהן הבסיס לניתוח פוריה, הן כידוע לא בעלות משך סופי. הן גם חלקות וצפויות, בעוד גלונים הינם אי-רגולרים באופיים, וא-סימטריים.
מספר משפחות של גלונים נמצאו כיעילות במיוחד, למשל:
Haar, Daubechues, Biorthogonal, Coiflets, Symlets, Morlet ועוד. ניתן לחקור אותן באמצעות ה-Wavelet Toolbox, וכמובן להשתמש בו על מנת לבצע ניתוח Wavelet תוך שימוש בהן.
אז מה זה בעצם ה-Wavelet Toolbox
Wavelet Toolbox הוא אוסף של פונקציות הפועל בסביבת המיחשוב הטכני של MATLAB, והמאפשר לבצע ניתוח בשיטת Wavelet. בין היתר, ה-Toolbox מאפשר:
• לבחון ולחקור מאפיינים של גלונים בודדים ושל Wavelet packets
• לחקור סטטיסטיקה של אותות ושל מרכיבי אותות
• לבצע התמרת Wavelet רציפה על סיגנל חד-מימדי
• לבצע פירוק והרכבה של אותות חד ודו מימדיים (בדידים)
• לבצע ניתוחי Wavelet packet לאותות חד ודו מימדיים
• לדחוס ולהסיר רעש מאותות ותמונות
ה-Toolbox מספק שני סוגים של כלים:
• פונקציות שהן בעצם m-files שאפשר להשתמש בהן בשורת הפקודה או בסקריפט,
• ממשקים גרפיים אינטראקטיביים (העלאה ע"י פקודת wavemenu או על ידי בחירה
ב-App המתאים בגלריית ה-Apps החל מגרסת R2012b), דוגמאות לשנים מהם מובאות להלן:
האם הכרתם את תורת הגלונים לפני הפוסט הזה? האם יצא לכם להשתמש ב-Wavelet Toolbox? האם השתמשתם בפונקציות שבו או בממשק הגרפי שלו?
היום בעידן ה BIG DATA הוצאת המוץ מן התבן חשובה לא פחות מכריית המידע. לכן הפונקציה של לדחוס ולהסיר רעש מאותות ותמונות היא אחת מהחשובות ביותר במערכות Wavelet Toolbox
השבמחק